★고어매니아★들을 위한 리버의 고어영화 추천 리스트!!!
※이 영화들은 정신건강에 딱히 좋지 않으니 진짜 고어매니아들만 보길 바람※
.
.
.
.
.
.
.
.
.
.

학살된 구토인형들(2006)
이 영화를 보려고 했지만 파일을 당최 찾을 수가 없어서 너무 궁금하다. 만약 본다면 너무 잔인해서가 아니라 너무 더러워서 보다가 끌 것으로 예상... 솔직히 말해서 쓰레기 식욕감퇴 영화가 맞다. 그래서 고어 매니아들에게만 추천드린다.

그로테스크(2009)
내가 학창시절 처음으로 접했던 제대로 된 고어 영화라고 할 수 있다. 그래도 쏘우 등 잔인한 영화를 많이 봤었던 터라 딱히 기대안하고 봤었는데 와우... 지금까지 본 그저 잔인한 영화가 아닌 쏘우는 쨉도 안되는 다른 차원의 잔인함의 영화여서 충격받았다. 상상력을 뛰어넘어 창의적으로 고문하는 고어영화 그로테스크 추천해본다.

더 포킵시 테잎스(2007)
사이코패스의 살인 스토리를 찍은 페이크 다큐멘터리 영화고 개봉금지 판정을 받았다. 유명한 움짤인 네발로 기어 다니는 사람은 정말 기괴하고 기분 나쁨... 스너프 필름 같은 고어 영화 좋아하는 사람은 한번 볼 것을 추천함.

마터스(2008)
군대에 있을 때 내가 보자고 해서 봤는데 영화가 끝나고 분대원 다들 패닉 상태에 빠진 영화. 진짜 이 이영화는 진짜 다 보고 나면 뭐 벙찔 수밖에 없다. 배우들이 참 대단하다 생각... 공포영화 매니아들도 충격에서 빠져나오는데 오래 걸렸다는 영화 마터스 도전해봐라.

살로 소돔의 120일(1975)
아마 고어매니아들이라면 한 번쯤은 들어본 영화라고 생각한다. 영화에서 권력자들의 쾌락을 위해서 별짓을 다하는데 가관이며 아마 사디즘의 시초가 된 영화가 아닐까 싶다. 이 영화감독이 영화 출연배우 애인한테 살해당했다고 함. 그만큼 말도 많고 탈도 많은 상식을 벗어난 영화. 개인적으로 나는 잔인한 것보다 되게 더럽다고 느꼈음.

세르비안 필름(2010)
역시 많은 국가에서 상영금지 처분을 받은 충격적이고 자극적인 영화. 강간, 살인, 근친상간 등 추악한 요소가 다 나오는 스너프 필름식 영화이니 마음의 준비를 하고 보길 바란다. 도대체 세르비아가 감독에게 어떤 이미지길래 이 정도로 표현했는지 궁금...

쇼군의 새디즘(1976)
남성과 여성을 상대로 살인, 온갖 별의별 방식으로 고문하는 이상하고 딱히 내용 없는 영화라 말하고 싶다. 고어물을 찾다가 발견한 작품인데 진짜 사진에서 보시다시피 저놈 진짜 싸이코 연기 대단하다 라는 생각함. 개봉연도를 보다시피 되게 옛날 작품인데 당시 얼마나 일본 사회가 비인간적이었을까 생각함.

스너프 102(2007)
페이크 다큐멘터리 형식으로 매우 사실적으로 영화를 찍어서 실제로 오해를 많이 받은 영화다. 이것도 뭐 다른 영화와 마찬가지로 온갖 추악한 요소들을 결합한 잔혹함의 끝판왕... 일반적인 고어 영화로는 만족이 안 되는 사람들을 위한 스너프 영화라 말하고 싶다.

여학(1996)
페이스북 같은 매체에서도 많이 봤을 거라 생각하는 손 튀김 장면 이 영화가 바로 유명한 일본고어 영화 여학이다. 대충 고통을 받으면 쾌락을 느끼는 영환데 자신에게 고통을 주며 자해하는 수위가 점점 높아져서 놀라움. 한번 봤을까싶은 그로테스크한 장면들이 꽤 많을거라 생각해서 고어를 좋아하는 사람들은 제대로 봐보는걸 추천한다.

위대한 실험(2003)
고어영화 1위라고 많이 알려져 있는 아주 유명한 제목의 고어 영화다. 진짜 잔혹하고 더럽고 거칠어서 웬만하게 고어 영화에 단련되어있어도 보기 힘들다는 평이 많아 나도 살짝 쫄려서 감히 찾아서 볼 생각을 못했었다. 근데 군대에서 핸드폰으로 어떻게 용기 내어 봤는데 자막도 없고 뭐 그냥 어지러운 연출에... 다 보고 느낀 건 이것은 여태껏 본 것 중 진정한 쓰레기 고어 영화. 궁금한 사람은 뭐 한번 봐도 나쁘지 않을 것 같으니 추천함.

피를 빠는 변태들(1978)
그냥 고문 그 자체인 영화. 제목에서부터 티 나듯이 매우 선정적이며 잔혹하다. 딱히 할 말이 없다. 길이길이 남을 고전 고어 레전드 영화이니 한번 보자.

기니어 피그 : 혈육의 꽃(1985)
고등학교 때 봤었는데 몇 년이 지난 지금도 고문하는 아저씨의 창백하고 하얀 무서운 얼굴이 트라우마로 남아있다...ㅠㅠ 총 3개의 기니어 피그 시리즈 중 가장 레전드로 꼽히는 작품으로 한 영화배우가 실제인 줄 알고 신고했다는 유명한 썰이 있음. 여자 하나 가지고 온갖 미친 짓을 하는데 진짜 웬만한 정신력 아니면 이건 보지 않는 걸 추천한다.

호스텔(2005)
슬로바키아를 완전 이상한 곳으로 만들어서 정부의 항의를 받은 유명한 영화. 실제로는 범죄율이 높지 않다. 위에서 설명한 고어 영화랑 비교하면 수위가 낮은 편이라 수월하게 볼 수 있을 것이니 한번 보는 걸 추천한다. 물론 평범한 사람이 본다면 무척이나 잔인함.

카니발 홀로코스트(1980)
원주민과 정글에서 벌어지는 일이라 그런지 그린 인페르노라는 영화하고 헷갈려하는 사람들이 많다. 이 영화 역시 충격적인 영상이 많아 많은 나라에서 상영금지를 당했고 감독이 실제로 배우를 살해한 거 아니냐는 의혹을 받아 종신형을 받을 뻔한 사건도 있었다. 옛날 영화지만 그만큼 원주민들과 벌어지는 스토리와 영상이 레전드 급이기 때문에 고어매니아들이라면 한 번쯤은 봤을 영화다.

휴먼 센티피드 시리즈 1,2,3(2009,2011,2015)
대중들에게도 많이 알려져 있는 유명한 고어 영화 인간 지네 시리즈 그래서인지 많은 곳에 패러디로 자주 등장한다. 뭐 이 영화는 다들 내용을 대략 알고 있을 거라 생각한다. 개인적으로 나는 2편이 가장 끔찍하고 더러웠었다.
BONUS 고어 애니메이션 추천


엘펜리트(2004), 콥스파티OVA(2013)
고어매니아들은 공감 클릭 부탁드려요 ~ ~ ~
'영화' 카테고리의 다른 글
| 한번쯤은 볼만한 스릴러 영화 추천 Ⅴ (2) | 2020.10.19 |
|---|---|
| 한번쯤은 볼만한 스릴러 영화 추천 Ⅵ (0) | 2020.10.05 |
| 한번쯤은 볼만한 스릴러 영화 추천 Ⅲ (0) | 2020.10.05 |
| 한번쯤은 볼만한 스릴러 영화 추천 Ⅱ (0) | 2020.09.05 |
| 한번쯤은 볼만한 스릴러 영화 추천Ⅰ (0) | 2019.01.06 |


































































































































































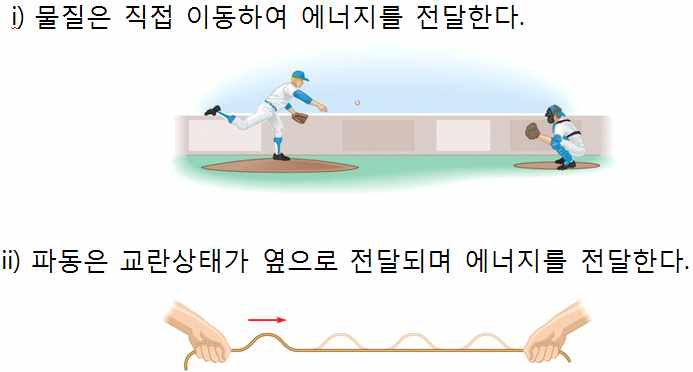






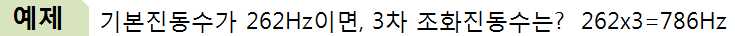


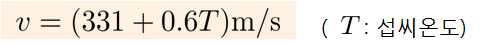










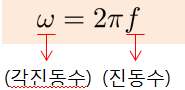
































































































































































































































 퀴즈 7.pdf
퀴즈 7.pdf






































































































